szerző: Fényes Dániel

Modellezés

2.1. Felfüggesztés modellezése

2.1.1. SimMechanics modell

A futómű kinematikai viszonyainak vizsgálatához elkészítésre került a szerkezet 3 dimenziós modellje Matlab SimMechanics szimulációs környezetben. A paramétereket úgy választottam meg, hogy a felfüggesztés kormánylegördülési sugara alapesetben nulla értékű legyen. Az aktuátor helyén egy csuklót helyeztem el, ezzel biztosítva a későbbi beavatkozás helyét. A modell bizonyos paraméterei (tömeg, csillapítás, rugómerevség) a CarSim program értékei alapján lettek meghatározva. A kerék dőlése esetén keletkező oldalirányú erő a következő modellel lett definiálva:

Ahol az R a keréksugár, C az oldalirányú kerékmerevség, v a jármű sebessége, φ pedig a kerékdőlés. A gumi rugalmasságát egy a talaj és a kerékfelfekvési pontja közé helyezett már a terhelés áltál deformált rugó-csillapító taggal modelleztem. A gumi csillapítása a vizsgálat során elhanyagolásra került. E tagot úgy láttam el kényszerekkel, hogy a benne keletkező erő iránya párhuzamos legyen a kerék hossztengelyével. A felfüggesztés rugó-csillapító tagja a modellezés során két részre lett bontva. Az első merev rész látható a 2.1-es ábra jobb felső részén, a második része egy rugó-csillapító tag volt, amely egyik végét a merev tag végpontjához, a másik végét pedig egy elhanyagolható tömegű tömegponthoz kötöttem, mivel csak tömeggel rendelkező testet lehet kényszerrel ellátni, így biztosítva a végpont a tér mindhárom irányába történő elfordulását. Természetesen ez a tag is deformált állapotban került modellezésre. Az alsó lengőkar egyik végpontjához szintén elhanyagolható tömegű tömegpontokhoz lett rögzítve, egy-egy csuklót közbeiktatva, amely (z) irányú elfordulást tesz lehetővé, másik végpontjának elmozdulása szintén egy csukló elhelyezésével lett biztosítva. A felfüggesztés többi csatlakozási pontja között merev kapcsolat van.

2.1.2. Nemlineáris modell

A rendszer irányítástervezéséhez szükséges a felfüggesztés dinamikai viszonyainak meghatározása. E célból felírásra került a modell beavatkozási pontjára (2.1 ábra) (A) pontjára a (z) irányú nyomaték, illetve az (y) irányú erőegyenletek.

Nem lineáris modell kiértékelése

A továbblépéshez elengedhetetlen a felírt modell paramétereinek a becslése, e célból mindkét modellre ugyanazokat a vizsgálójeleket kapcsoltam bemenetként és összevetettem a létrejövő kerékdőlési függvényeket, mint kimeneteket.

Szinusz

Az első vizsgálójel egy 1200 Nm amplitúdójú, 400 Nm eltolású és 4 rad/s frekvenciájú szinusz jel volt. A bemeneti függvény az 2.3. ábrán, a válaszfüggvények a 2.4. ábrán láthatóak. A második ábráról leolvasható, hogy a két függvénynek mind az amplitúdója, mind a frekvenciája nagyon kis eltérést mutat.

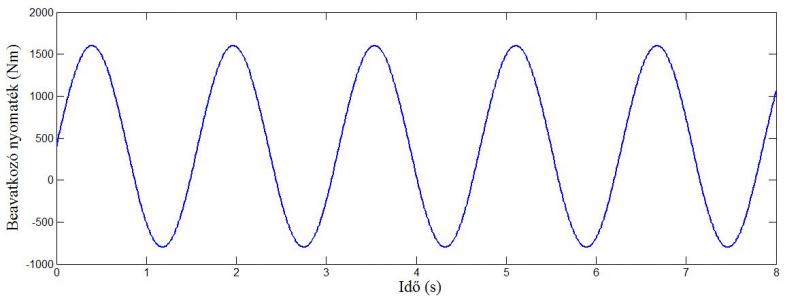
2.3. ábra Szinusz vizsgálójel

2.4. ábra Szinusz válaszfüggvénye

Chirp

A második vizsgálójel egy 0.1 Hz es kezdőfrekvenciájú, 2 Hz-es beállási frekvenciájú és 15 másodperces célidejű 1200 Nm-es erősítésű és 400 Nm eltolású Chirp jel volt. A bemenő jel a 2.5. ábrán, a modellek válaszfüggvényei a 2.6. ábrán láthatóak. A második ábráról leolvasható, hogy a két modell különböző frekvenciájú jelek esetén is jól fedi egymást.

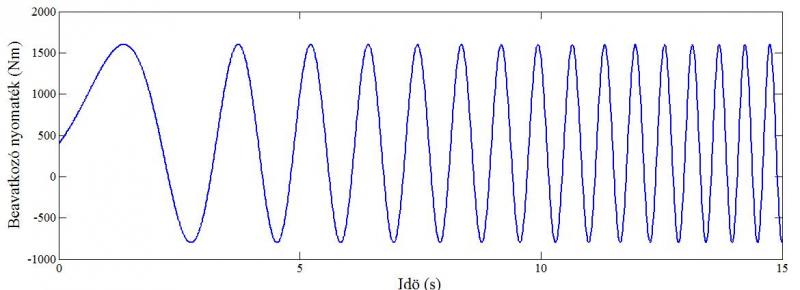
2.5. ábra Chirp vizsgálójel

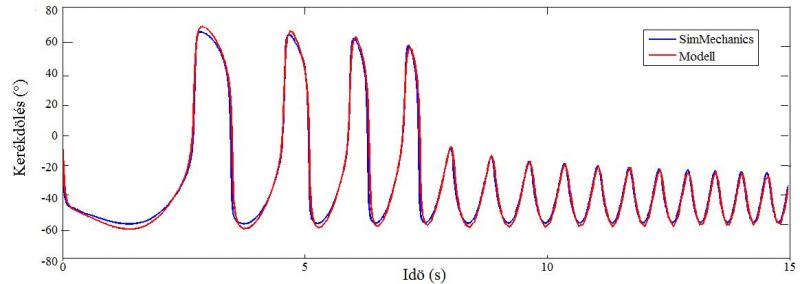
2.6. ábra Chirp válaszfüggvénye

Konstans bemenet

A negyedik vizsgálójel egy konstans -290 Nm értékű jel volt. A bemenő jel a 2.7-es ábrán, a modellek válaszfüggvényei a 2.8-as ábrán láthatóak.  

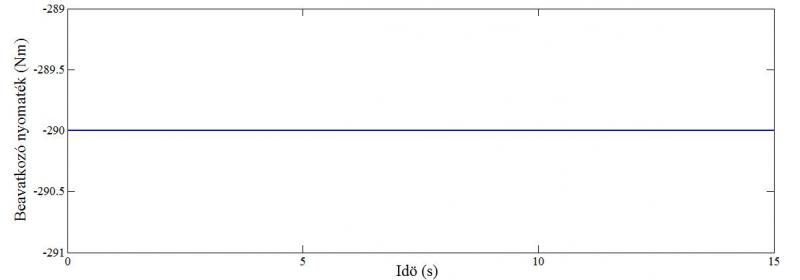
2.7. ábra Konstans vizsgálójel

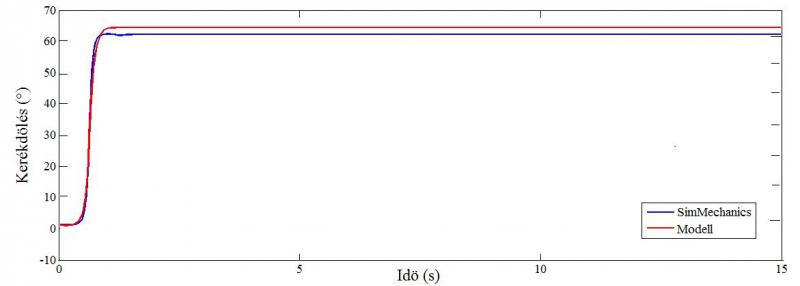
2.8. ábra Konstans válaszfüggvénye

Konklúzió

A Szinusz és Chirp jelekből látható, hogy a két modell között elhanyagolható fáziseltolás van. A konstans jelet úgy választottam meg, hogy közel kiindulási helyzetben tartsa a modelleket, ez meg is figyelhető az ábrán, körülbelül 0.3 másodpercig nem jön létre kerékdőlés. Ugyanezen az ábrán látható, hogy a modellek beállási értekének eltérése ≈6-8%. Összességében elmondható, hogy a felírt modell jól közelítése a SimMechanics-ban létrehozott modellnek.

A cikket folytatjuk. A cikk a szerző TDK dolgozatának része. A kutatómunkát a részletes számítások elhagyásával, egyébként tartalmi változtatások nélkül tettük közzé.

konzulens: Dr. Németh Balázs, Magyar Tudományos Akadémia, Számítástechnikai és Automatizálási Kutató Intézet